假設我們遇到如下問題：①對于M個方案，每個方案有N個屬性，在已知各個方案每個屬性值&&任意兩個屬性的重要程度的前提下，如何選擇最優的方案？②對于一個層級結構，在已知各底層指標相互之間的重要程度下，如何確定各底層指標對最高級指標的權值？… …此時，便可用層次分析法將我們的主觀想法——“誰比誰重要”轉換為客觀度量——“權值”

層次分析法的基本思想是將復雜問題分為若干層次和若干因素，在同一層次的各要素之間簡單地進行比較判斷和計算，并評估每層評價指標對上一層評價指標的重要程度，確定因素權重，從而為選擇最優方案提出依據。步驟如下：

（1）根據自己體系中的關聯及隸屬關系構建有層次的結構模型，一般分為三層，分別為最高層、中間層和最低層。

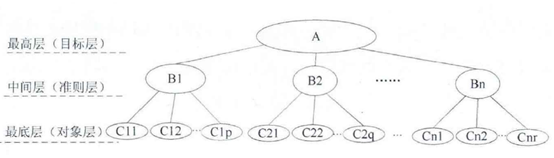
（2）構造判斷矩陣

假設該層有n個評價指標u1, u2, …, un，設cij為ui相對于uj的重要程度，根據公式列出的1-9標度法，判斷兩兩評價指標之間的重要性。

根據比較得出判斷矩陣：C=(cij)n*n其屬性為cij>0, cji=1/cij,cii=1

（3）層次單排序：從下往上，對于每一層的每個判斷矩陣，計算權向量和一致性檢驗。計算矩陣C的最大特征根λmax及對應的特征向量(P1,P2,…, Pn)

一致性指標定義為：

CI(Consistency Ratio)稱為一致性比例。CI=0時，具有完全一致性;CI接近于0，具有滿意的一致性;CI越大，不一致性越嚴重。

一致性比率定義為：

其中RI稱為隨機性指標，參照表如下：

只有當CR<0.1，則認為該判斷矩陣通過了一致性檢驗，即該矩陣自相矛盾產生的誤差可忽略。將矩陣C最大特征根對應的特征向量元素作歸一化處理，即可得到對應的權重集(C1,C2,…,Cn)。

（4）層次總排序

從上往下，依次計算每一層各指標對最上層指標的權值，以及每一層的綜合一致性比率CR。

由于層次分析法選用1-9標度構建判斷矩陣，而大部分時候我們自己也不能很好度量重要性的程度，故趙中奇提出用-1，0，1三標度來構建判斷矩陣。同時，自動調整判斷矩陣，消除前后時刻主觀比較重要性時的矛盾現象，即讓矩陣變為一致性矩陣（CR=0）。構建并調整判斷矩陣以及算權值向量的步驟如下：

（1）初始化m=1a、確定比較矩陣C=(cij)n*n的第m行元素

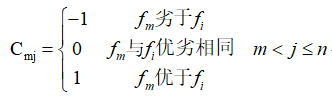
b、劃分指標集合Dm={j|j=m+1,…,n}為Hm={j|cmj=-1,j∈Dm}、Mm ={j|cmj=0,j∈Dm}與Lm={j|cmj=1,j∈Dm}

并構造集合為，其中×表示集合的笛卡爾積

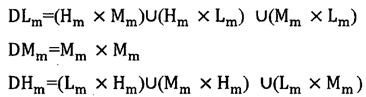
c、若DLm、DMm、DHm全為空集，轉d，否則令：

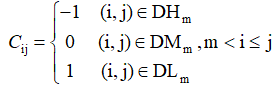
d、若m=n-1，轉第二步，否則令m=m+1，轉回a

（2）求比較矩陣C

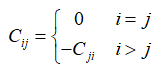
（3）求B=(bij)n*n，其中

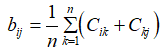
（4）求A=(aij)n*n的特征向量，作為各評價指標的相對權重值，其中:

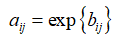
由于網上找到的代碼大多只能算三層的體系，而且沒有趙中奇論文中的自調節層次分析法代碼。因此，自己寫了一個可以計算超過3層的層次分析法和自調節層次分析法代碼！

構建如下4層體系

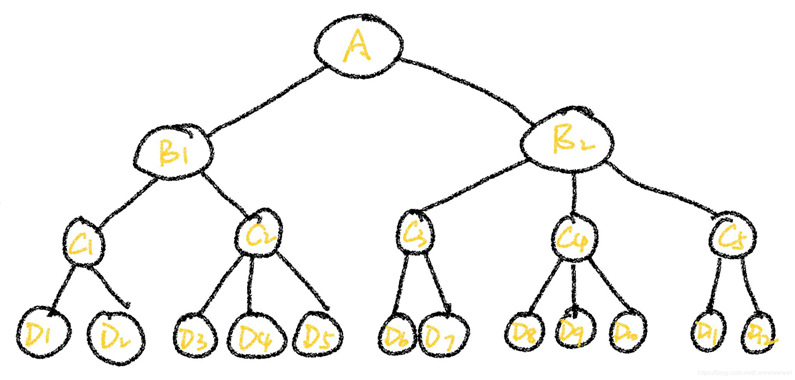
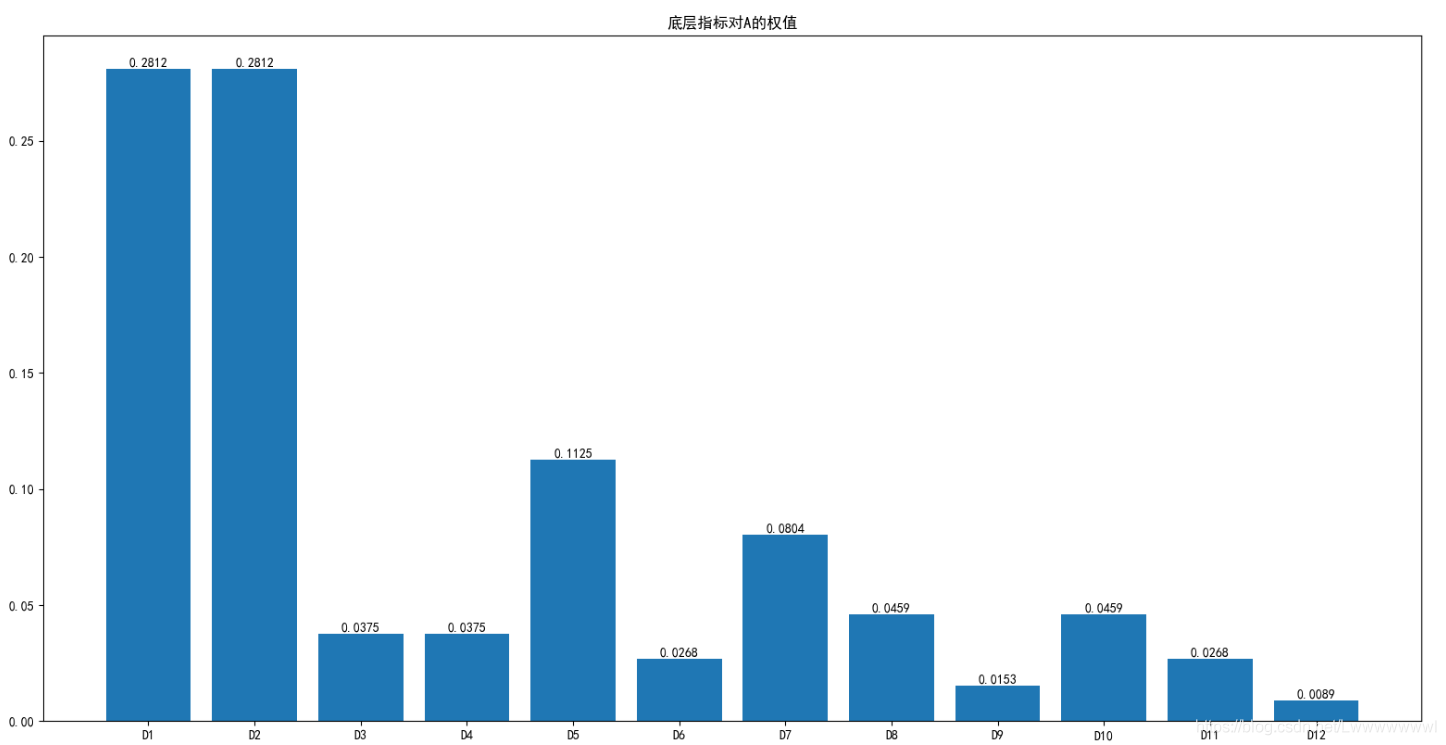
層次分析法得到的權值

判斷矩陣就不列出來了了，可以在代碼里找到，得到第四層對A的權值條形圖如下：

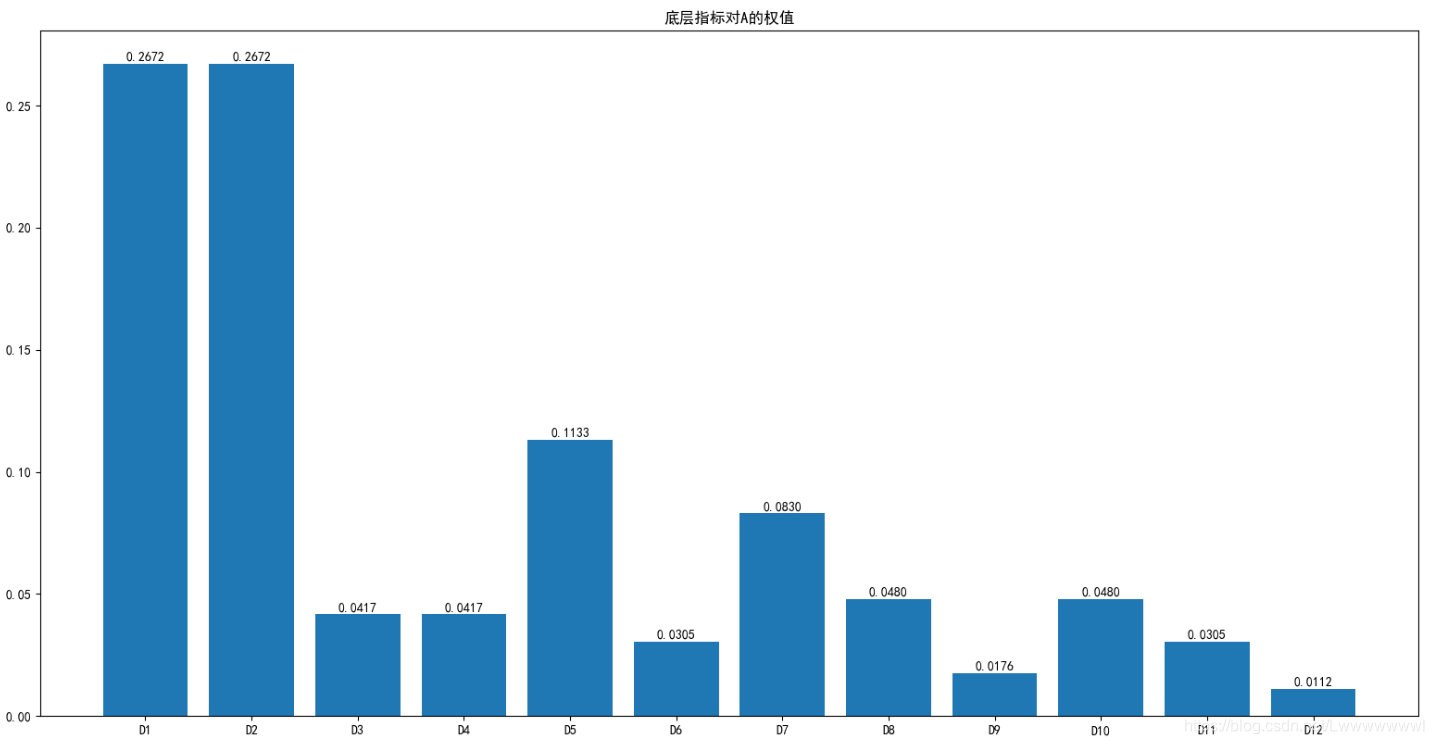
自調節層次分析法得到的權值

自調節層次分析法對高階判斷矩陣更有優勢，而算低階判斷矩陣時的結果和層次分析法差不多。

代碼包括了層次分析法與自調節層次分析法的實例，運行的時候注釋掉其中一個就行！

'''Created on Tue Jan 26 10:12:30 2021自適應層數的層次分析法求權值@author: lw'''import numpy as npimport itertoolsimport matplotlib.pyplot as plt#自適應層數的層次分析法class AHP(): ’’’ 注意：python中list與array運算不一樣，嚴格按照格式輸入！ 本層次分析法每個判斷矩陣不得超過9階，各判斷矩陣必須是正互反矩陣 FA_mx：下一層對上一層的判斷矩陣集（包含多個三維數組，默認從目標層向方案層依次輸入判斷矩陣。同層的判斷矩陣按順序排列，且上層指標不共用下層指標） string：默認為’norm’（經典的層次分析法，需輸入9標度判斷矩陣），若為’auto’（自調節層次分析法，需輸入3標度判斷矩陣） ’’’#初始化函數 def __init__(self,FA_mx,string=’norm’):self.RI=np.array([0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45,1.49]) #平均隨機一致性指標if string==’norm’: self.FA_mx=FA_mx #所有層級的判斷矩陣elif string==’auto’: self.FA_mx=[] for i in range(len(FA_mx)): temp=[] for j in range(len(FA_mx[i])): temp.append(self.preprocess(FA_mx[i][j])) self.FA_mx.append(temp) #自調節層次分析法預處理后的所有層級的判斷矩陣self.layer_num=len(FA_mx) #層級數目self.w=[] #所有層級的權值向量self.CR=[] #所有層級的單排序一致性比例self.CI=[] #所有層級下每個矩陣的一致性指標self.RI_all=[] #所有層級下每個矩陣的平均隨機一致性指標self.CR_all=[] #所有層級的總排序一致性比例self.w_all=[] #所有層級指標對目標的權值 #輸入單個矩陣算權值并一致性檢驗(特征根法精確求解) def count_w(self,mx):n=mx.shape[0]eig_value, eigen_vectors=np.linalg.eig(mx)maxeig=np.max(eig_value) #最大特征值maxindex=np.argmax(eig_value) #最大特征值對應的特征向量eig_w=eigen_vectors[:,maxindex]/sum(eigen_vectors[:,maxindex]) #權值向量CI=(maxeig-n)/(n-1)RI=self.RI[n-1]if(n<=2 and CI==0):CR=0.0else: CR=CI/RIif(CR<0.1): return CI,RI,CR,list(eig_w.T)else: print(’該%d階矩陣一致性檢驗不通過,CR為%.3f’%(n,CR)) return -1.0,-1.0,-1.0,-1.0#計算單層的所有權值與CR def onelayer_up(self,onelayer_mx,index):num=len(onelayer_mx) #該層矩陣個數CI_temp=[]RI_temp=[]CR_temp=[]w_temp=[]for i in range(num): CI,RI,CR,eig_w=self.count_w(onelayer_mx[i]) if(CR>0.1):print(’第%d層的第%d個矩陣未通過一致性檢驗’%(index,i+1))return CI_temp.append(CI) RI_temp.append(RI) CR_temp.append(CR) w_temp.append(eig_w)self.CI.append(CI_temp)self.RI_all.append(RI_temp)self.CR.append(CR_temp)self.w.append(w_temp) #計算單層的總排序及該層總的一致性比例 def alllayer_down(self):self.CR_all.append(self.CR[self.layer_num-1])self.w_all.append(self.w[self.layer_num-1])for i in range(self.layer_num-2,-1,-1): if(i==self.layer_num-2):temp=sum(self.w[self.layer_num-1],[]) #列表降維，扁平化處理，取上一層的權值向量 CR_temp=[] w_temp=[] CR=sum(np.array(self.CI[i])*np.array(temp))/sum(np.array(self.RI_all[i])*np.array(temp)) if(CR>0.1):print(’第%d層的總排序未通過一致性檢驗’%(self.layer_num-i))return for j in range(len(self.w[i])):shu=temp[j]w_temp.append(list(shu*np.array(self.w[i][j]))) temp=sum(w_temp,[])#列表降維，扁平化處理，取上一層的總排序權值向量 CR_temp.append(CR) self.CR_all.append(CR_temp) self.w_all.append(w_temp)return #計算所有層的權值與CR,層次總排序 def run(self):for i in range(self.layer_num,0,-1): self.onelayer_up(self.FA_mx[i-1],i)self.alllayer_down()return #自調節層次分析法的矩陣預處理過程 def preprocess(self,mx):temp=np.array(mx)n=temp.shape[0]for i in range(n-1): H=[j for j,x in enumerate(temp[i]) if j>i and x==-1] M=[j for j,x in enumerate(temp[i]) if j>i and x==0] L=[j for j,x in enumerate(temp[i]) if j>i and x==1] DL=sum([[i for i in itertools.product(H,M)],[i for i in itertools.product(H,L)],[i for i in itertools.product(M,L)]],[]) DM=[i for i in itertools.product(M,M)] DH=sum([[i for i in itertools.product(L,H)],[i for i in itertools.product(M,H)],[i for i in itertools.product(L,M)]],[]) if DL:for j in DL: if(j[0]<j[1] and i<j[0]): temp[int(j[0])][int(j[1])]=1 if DM:for j in DM: if(j[0]<j[1] and i<j[0]): temp[int(j[0])][int(j[1])]=0 if DH:for j in DH: if(j[0]<j[1] and i<j[0]): temp[int(j[0])][int(j[1])]=-1for i in range(n): for j in range(i+1,n):temp[j][i]=-temp[i][j]A=[]for i in range(n): atemp=[] for j in range(n):a0=0for k in range(n): a0+=temp[i][k]+temp[k][j]atemp.append(np.exp(a0/n)) A.append(atemp)return np.array(A) #%%測試函數if __name__==’__main__’ : ’’’ # 層次分析法的經典9標度矩陣 goal=[] #第一層的全部判斷矩陣 goal.append(np.array([[1, 3], [1/3 ,1]])) criteria1 = np.array([[1, 3], [1/3,1]]) criteria2=np.array([[1, 1,3],[1,1,3],[1/3,1/3,1]]) c_all=[criteria1,criteria2] #第二層的全部判斷矩陣 sample1 = np.array([[1, 1], [1, 1]]) sample2 = np.array([[1,1,1/3], [1,1,1/3],[3,3,1]]) sample3 = np.array([[1, 1/3], [3, 1]]) sample4 = np.array([[1,3,1], [1 / 3, 1, 1/3], [1,3, 1]]) sample5=np.array([[1,3],[1/3 ,1]]) sample_all=[sample1,sample2,sample3,sample4,sample5] #第三層的全部判斷矩陣 FA_mx=[goal,c_all,sample_all] A1=AHP(FA_mx) #經典層次分析法 A1.run() a=A1.CR #層次單排序的一致性比例（從下往上） b=A1.w #層次單排序的權值（從下往上） c=A1.CR_all #層次總排序的一致性比例（從上往下） d=A1.w_all#層次總排序的權值（從上往下） e=sum(d[len(d)-1],[]) #底層指標對目標層的權值 #可視化 plt.rcParams[’font.sans-serif’] = [’SimHei’] plt.rcParams[’axes.unicode_minus’] = False name=[’D1’,’D2’,’D3’,’D4’,’D5’,’D6’,’D7’,’D8’,’D9’,’D10’,’D11’,’D12’] plt.figure() plt.bar(name,e) for i,j in enumerate(e):plt.text(i,j+0.005,’%.4f’%(np.abs(j)),ha=’center’,va=’top’) plt.title(’底層指標對A的權值’) plt.show() ’’’#自調節層次分析法的3標度矩陣(求在線體系的權值) goal=[] #第一層的全部判斷矩陣 goal.append(np.array([[0, 1], [-1,0]])) criteria1 = np.array([[0, 1], [-1,0]]) criteria2=np.array([[0, 0,1],[0,0,1],[-1,-1,0]]) c_all=[criteria1,criteria2] #第二層的全部判斷矩陣 sample1 = np.array([[0, 0], [0, 0]]) sample2 = np.array([[0,0,-1], [0,0,-1],[1,1,0]]) sample3 = np.array([[0, -1], [1, 0]]) sample4 = np.array([[0,1,0], [-1, 0,-1], [0,1,0]]) sample5=np.array([[0,1],[-1 ,0]]) sample_all=[sample1,sample2,sample3,sample4,sample5] #第三層的全部判斷矩陣 FA_mx=[goal,c_all,sample_all] A1=AHP(FA_mx,’auto’) #經典層次分析法 A1.run() a=A1.CR #層次單排序的一致性比例（從下往上） b=A1.w #層次單排序的權值（從下往上） c=A1.CR_all #層次總排序的一致性比例（從上往下） d=A1.w_all#層次總排序的權值（從上往下） e=sum(d[len(d)-1],[]) #底層指標對目標層的權值 #可視化 plt.rcParams[’font.sans-serif’] = [’SimHei’] plt.rcParams[’axes.unicode_minus’] = False name=[’D1’,’D2’,’D3’,’D4’,’D5’,’D6’,’D7’,’D8’,’D9’,’D10’,’D11’,’D12’] plt.figure() plt.bar(name,e) for i,j in enumerate(e):plt.text(i,j+0.005,’%.4f’%(np.abs(j)),ha=’center’,va=’top’) plt.title(’底層指標對A的權值’) plt.show()

到此這篇關于Python實現層次分析法及自調節層次分析法的示例的文章就介紹到這了,更多相關Python 層次分析法及自調節層次分析法內容請搜索好吧啦網以前的文章或繼續瀏覽下面的相關文章希望大家以后多多支持好吧啦網！