python 計算t分布的雙側置信區間
如下所示:
interval=stats.t.interval(a,b,mean,std)t分布的置信區 間
a:置信水平
b:檢驗量的自由度
mean:樣本均值
std:樣本標準差
from scipy import statsimport numpy as npx=[10.1,10,9.8,10.5,9.7,10.1,9.9,10.2,10.3,9.9]x1=np.array(x)mean=x1.mean()std=x1.std()interval=stats.t.interval(0.95,len(x)-1,mean,std)
intervalOut[9]: (9.531674678392644, 10.568325321607357)
補充:用Python學分析 - t分布
1. t分布形狀類似于標準正態分布
2. t分布是對稱分布,較正態分布離散度強,密度曲線較標準正態分布密度曲線更扁平
3. 對于大型樣本,t-值與z-值之間的差別很小
作用- t分布糾正了未知的真實標準差的不確定性
- t分布明確解釋了估計總體方差時樣本容量的影響,是適合任何樣本容量都可以使用的合適分布
應用- 根據小樣本來估計呈正態分布且方差未知的總體的均值
- 對于任何一種樣本容量,真正的平均值抽樣分布是t分布,因此,當存在疑問時,應使用t分布
樣本容量對分布的影響- 當樣本容量在 30-35之間時,t分布與標準正態分布難以區分
- 當樣本容量達到120時,t分布與標準正態分布實際上完全相同了
自由度df對分布的影響- 樣本方差使用一個估計的參數(平均值),所以計算置信區間時使用的t分布的自由度為 n - 1
- 由于引入額外的參數(自由度df),t分布比標準正態分布的方差更大(置信區間更寬)
- 與標準正態分布曲線相比,自由度df越小,t分布曲線愈平坦,曲線中間愈低,曲線雙側尾部翹得愈高
- 自由度df愈大,t分布曲線愈接近正態分布曲線,當自由度df= ∞ 時,t分布曲線為標準正態分布曲線
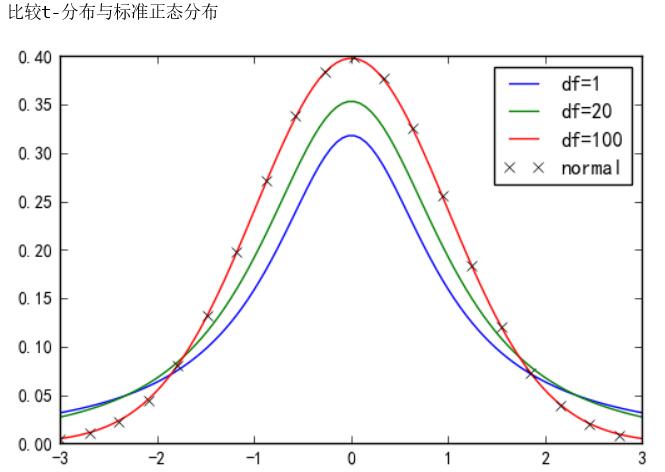
圖表顯示t分布代碼:
# 不同自由度的學生t分布與標準正態分布import numpy as npfrom scipy.stats import normfrom scipy.stats import timport matplotlib.pyplot as pltprint(’比較t-分布與標準正態分布’)x = np.linspace( -3, 3, 100)plt.plot(x, t.pdf(x,1), label=’df=1’)plt.plot(x, t.pdf(x,2), label=’df=20’)plt.plot(x, t.pdf(x,100), label = ’df=100’)plt.plot( x[::5], norm.pdf(x[::5]),’kx’, label=’normal’)plt.legend()plt.show()
運行結果:
以上為個人經驗,希望能給大家一個參考,也希望大家多多支持好吧啦網。如有錯誤或未考慮完全的地方,望不吝賜教。
相關文章:
1. 學python最電腦配置有要求么2. Spring security 自定義過濾器實現Json參數傳遞并兼容表單參數(實例代碼)3. JAMon(Java Application Monitor)備忘記4. Java8內存模型PermGen Metaspace實例解析5. python中用Scrapy實現定時爬蟲的實例講解6. 基于python實現操作git過程代碼解析7. python使用QQ郵箱實現自動發送郵件8. Python Scrapy多頁數據爬取實現過程解析9. 解決redis與Python交互取出來的是bytes類型的問題10. Python 的 __str__ 和 __repr__ 方法對比

 網公網安備
網公網安備